Stochastic Process/Stochastic Process

Ch2. Brownian Motion

LunaMooN 2022. 2. 7. 11:00

1. Random Walk

(1) 동전던지기 실험 예시

  • 앞면이 나올 확률과 뒷면이 나올 확률이 각각 1/2 인 경우

 

$ X_j =
\begin{cases}
1, & \mbox{if }w_j = Head \\
-1, & \mbox{if }w_j=Tail
\end{cases} $

  • $M_k = \sum_{j=1}^{k} X_j \quad (k=1,...) \quad M_0=0$
  • $E(M_k) = 0, \quad Var(X_j) = 1$
    • $k_0 < k_1< k_2 < ... < k_m$ 일 때, $M_{k_i+1} - M_{k_i} = \sum_{j=k_i+1}^{k_{i+1}} X_j$
  •  $E(M_{k_i+1} - M_{k_i}) = 0$
  • $Var(M_{k_i+1} - M_{k_i}) = \sum_{j=k_i+1}^{k_{i+1}} Var(X_j) = k_{i+1} - k_i$

 

(2) 금융에서의 random walk

  • Discrete Time Series
    • $X_t = X_{t-1} + \epsilon_t, \quad {\epsilon_t \sim i.i.d(0, \sigma^2)}$
      • $X_t = X_0 + \epsilon_1+\epsilon_2+ ... +\epsilon_t = X_0 + \sum_{j=1}^{t} \ \epsilon_j $
        • $ E[S_t]= X_0, \quad Var[S_t] = t \sigma^2 $

 

2. Brownian Motion

(1) 정의

  • Brownian Motion은 다음의 조건을 만족한다
    • $Prob(B_0=0)=1$
    • 임의의 $0 \leq t_1 < t_2 < ... $ 에 대하여 $B_{t_1}, B_{t_2}-B_{t_1},B_{t_2}-B_{t_1}, ...$ 은 서로 독립이다(Independence of increments).
    • $B_t - B_s \sim N(0, \sigma^2(t-s)), \quad 0 \leq s \leq t$
    • $\{B_t \}$: $t$ 에 관해 연속이다.

 

  • Random Walk에 스케일을 조정한 $X_t/\sqrt{n}$ 은 $n \rightarrow \infty $ 일 때, $B_t$ 로 수렴한다.
    • Wiener Process(혹은 Brownian Motion)은 Random walk의 t 사이사이에 더 작은 시간단위를 추가한 것이다. 이는 연속적인 시간 하의 금융시장에 적용될 수 있다.

 

(2) 특징

  • 브라운 운동의 증분 $W_{t+s} - W_s$ 는 이전 기간과 독립이다. 따라서 만약 $0 \leq v \leq s$ 인 $v$ 가 존재할 때 이는 $W_{t+s} - W_s$ 에 아무런 영향을 주지 않는다. (Markov Process)
  • 만약 $t > s$ 이면, $E[W_t | I_s] = W_s$ 이다. (Martingale Process)
  • $0 \leq s < t$ 에 대하여, $W_t - W_s \sim N(0, \sigma^2(t-s)), \quad W_{t-s} - W_0 \sim N(0, \sigma^2(t-s))$ 가 성립한다.
  • 미분이 불가능하다. 

 

(3) Simulation

import numpy as np
import matplotlib.pyplot as plt

 

3. Arithmetic Brownian Motion

(1) 정의

  • $d X_t = \mu dt + \sigma d W_t, \quad W_t \sim N(0, 1)$
    • 주가는 장기적으로 추세를 갖고 상승함
    • $\mu$ : drift term
  • $X_t = \mu + X_{t-1} + \epsilon_t$
    • $X_t = X_0 + \epsilon_1+\epsilon_2+ ... +\epsilon_t = S_0 + \sum_{j=1}^{t} \ \epsilon_j $

 

(2) Stochastic Differential Equation

\begin{eqnarray} \int_{0}^{T} d X_t = \int_{0}^{T} \mu dt + \int_{0}^{T} \sigma d W_t \\ X_T - X_0 = \mu(T-0) + \sigma (W_T - W_0), \\ X_T = X_0 + \mu T + \sigma W_T \end{eqnarray}

(3) Mean and Variance

  • $E[X_T] = X_0 + \mu T$
  • $Var[X_T] = \sigma^2 T$
  • $Cov[X_t, X_s] = \sigma^2 min(t, s)$

 

(4) Simulation

$d X_t = \mu dt + \sigma d W_t$ 를 통해 $\mu$와 $\sigma$를 추정한다.

$ X_T = X_0 + \mu T + \sigma W_T $ 에 추정된 값을 넣어 미래 시점의 X 값을 수만번 시뮬레이션 후 분포를 확인한다.

예시) 95% 신뢰수준에서 X 값이 어떤 boundary 안에 있을지 보고 그에 맞는 위험 관리를 할 수 있다.

import yfinance as yf
from Brownian_Motion import Brownian
import matplotlib.pyplot as plt

df = yf.download('KO', '2017-01-01', '2022-01-01').Close
model = Brownian(df, process='arithmetic', period='daily')
model.fit()
paths = []
for i in range(20):
    paths.append(model.predict(t=i))
paths = np.array(paths)
plt.plot(paths[:, :20])
plt.show()
prediction = model.predict(t=20)
plt.hist(prediction)
plt.show()
print(model.confidence_level_)

t=1,..,20 paths
t=20에서의 X 값 분포

 

(54.077968542154025, 64.95059117054961)

 

4. Geometric Brownian Motion

(1) 정의

  • $d X_t = \mu X_t dt + \sigma X_t dW_t, \quad W_t \sim N(0,1) $
    • 주가 수익률에 대한 확률과정
  • 주가의 변동에 따른 GBM 일반화 식 도출
    • 가정: 주가는 오르거나 내린다. 주가가 상승할 확률을 H, 하락할 확률을 T라고 하자. (위에서 동전 던지기의 H, T라고 생각하면 좀 더 이해가 쉽다.)
    • $S_t = S_0 \left(1 + \frac{\mu}{n}+ \frac{\sqrt{\sigma}}{n} \right)^H \left(1 + \frac{\mu}{n}- \frac{\sqrt{\sigma}}{n} \right)^T$
      • $\mu$: drift
      • $\sigma$: return (주가의 순간 분산은 수익률 제곱이로 순간 표준편차는 수익률)
  • $nt = H + T, \quad M = H- T$
    • $M$ 은 랜덤워크를 따름(위의 2.0에서 $M_k$ 의 정의를 보면 알 수 있음)
  • $S_t = S_0 \left( 1 + \frac{\mu}{n}+ \frac{\sigma}{\sqrt{n}}\right)^{\frac12(nt+M)} \left( 1 + \frac{\mu}{n}- \frac{\sigma}{\sqrt{n}}\right)^{\frac12(nt-M)}$
    • $H= \frac12(nt+M), \quad T=\frac12(nt-M)$
  • $ \ln{S_t} = \ln{S_0} + \mu t - \frac{\sigma^2}{2} t + \sigma W_t$
    • $\ln \left( 1+ \frac{\mu}{n} + \frac{\sigma}{\sqrt{n}} \right) \approx \left( \frac{\mu}{n} + \frac{\sigma}{\sqrt{n}} \right)- {1 \over 2}\left( \frac{\mu}{n} + \frac{\sigma}{\sqrt{n}} \right)^2$
    • $\ln \left( 1+ \frac{\mu}{n} - \frac{\sigma}{\sqrt{n}} \right) \approx \left( \frac{\mu}{n} - \frac{\sigma}{\sqrt{n}} \right)- {1 \over 2}\left( \frac{\mu}{n} - \frac{\sigma}{\sqrt{n}} \right)^2$
      • By Taylor's Series
    • $n \rightarrow \infty: \frac{M}{\sqrt{n}} = W_t$: 무한번 동전던지기 게임을 하면 랜덤워크 과정은 위너과정이 됨
  • 따라서, $ S_t = S_0 e^{\sigma W_t + \left(\mu - \frac{\sigma^2}{2} \right) t} $ 가 기하브라운운동(GBM)의 식이 된다

 

(2) Stochastic Differential Equation

\begin{eqnarray} dX_t = \mu X_t dt + \sigma X_t dW_t, \quad \\ dY_t = d \ln X_t = \frac{d X_t}{X_t} - \frac12 \frac{dX_t ^2}{X_t ^2} \leftarrow dX_t ^2 = \sigma^2 X_t ^2 dt \\ d \ln X_t = \mu dt + \sigma d W_t - \frac12 sigma^2 dt \\ d \ln X_t = \left( \mu - \frac{\sigma^2}{2} \right) dt + \sigma dW_t  \\ \int_{0}^{T} d \ln X_t = \int_{0}^{T} \mu - \frac{\sigma^2}{2} dt + \int_{0}^{
T} \sigma dW_t \\ \ln X_t - \ln X_0 = \left(\mu - \frac{\sigma^2}{2} \right)T + \sigma W_T \end{eqnarray}

 

(3) Mean and Variance

  • $E[\ln X_t] = \ln X_0 + \left(\mu - \frac12 {\sigma^2} \right)t $
  • $Var[\ln X_t] = \sigma^2 T$
  • $Cov[X_t, X_s] = X_0^2 e^{\mu(t+s)}$

 

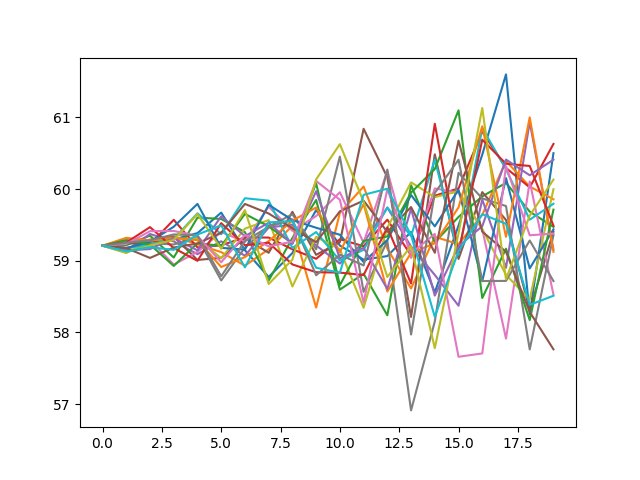
(4) Simulation

import yfinance as yf
from Brownian_Motion import Brownian
import matplotlib.pyplot as plt

df = yf.download('KO', '2017-01-01', '2022-01-01').Close
model = Brownian(df, process='geometric', period='daily')
model.fit()
paths = []
for i in range(20):
    paths.append(model.predict(t=i))
paths = np.array(paths)
plt.plot(paths[:, :20])
plt.show()
prediction = model.predict(t=20)
plt.hist(prediction)
plt.show()
print(model.confidence_level_)

 

t=1,..,20 paths

 

t=20에서의 X 값의 분포

[57.69536717 61.45777074]

 

5. Fractional Brownian Motion

(1) 정의

  • Brownian Motion의 일반화된 확률 과정
  • Independent Increment 가정 성립하지 않음
    • $Cov[B_H(t), B_H(s)]=E[B_H(t) B_H(s)] = \frac12 (|t|^{2H}+ |s|^{2H} - |t-s|^{2H})$ : H는 Hurst Index

 

(2) 특징

  • Hurst index에 따라 Process가 결정됨 

 

$ B_H(t) =
\begin{cases}
\text{Wiener Process}, & \mbox{if }H= 1/2 \\
\text{Mean-reverting}, & \mbox{if }H<1/2 \\ \text{Trending}, & \mbox{if }H>1/2 \\ \end{cases} $

 

Proof

\begin{eqnarray} & \text{For } 0 \leq s_1 < t_1 < s_2 < t_2, \quad [s_1, t_1] \cap [s_2, t_2] = \varnothing \\ & E[(B_H(t_1)-B_H(s_1))(B_H(t_2)-B_H(s_2)] = \frac12 (|t_2 - s_1|^{2H} - |t_2-t_1|^{2H} - (|s_2 -s_1|^{2H} - |s_2 - t_2|^{2H})) \\ & \text{Map } f(x) = x^{2H} \text{then } E[(B_H(t_1)-B_H(s_1))(B_H(t_2)-B_H(s_2)] = \frac12 (f(a_1)-f(a_2) -(f(b_1)- f(b_2)) \\ & (a_1=t_2-s_1, \; a_2 = t_2-t_1, \; b_1 = s_2-s_1, \; b_2=s_2-t_2, \quad \text{and } \quad  b_2<a_2<b_1<a_1) \\ \\ & \text{For } H \in (0, 1/2) \quad f'' <0, \quad E[.] <0 \rightarrow \text{negatively correlated} \\ & \text{For } H \in (1/2, 1) \quad f'' >0, \quad E[.] >0 \rightarrow \text{positively correlated} \end{eqnarray}

 

 

 

 

 

https://github.com/HEEJOOMOON/Stochastic_Process